زوايا الارتفاع و الانخفاض

من اهم ميزات TI-nspire هو قدرة المعلم على وضع خطوات الحل بالتدريج لطلبته بحيث ينفذونها خطوة بخطوة و عرض مايريد من توضيحات و مفاهيم قبلية لطلبته قبل ان يبدأ بالمفهوم الجديد

الدرس التالي هو عن زوايا الارتفاع و الانخفاض حرص فيه المؤلف على توضيح مفهوم المثلث القائم و الدوال المثلثية المتعلقة به قبل شرح مفهوم هذه الزوايا الذي وضعه بالخطوات المصورة 

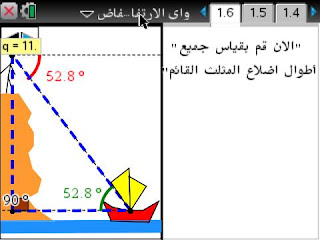
الصور التالية تمثل بعض صفحات هذا الدرس 

لتحميل الدرس المعرب انضم الى مركز تبادل أنشطةTI-nspire بالعربي على facebook

https://www.facebook.com/groups/431632803585176/

اقرأ المزيد;

اثبات المتطابقات المثلثية

 س: ماهي المتطابقات  المثلثية ؟؟
ج : هي عبارات رياضية عن الدوال المثلثية و هي صحيحة دائما



س: كيف يمكن اثبات صحتها ؟
ج: يمكنك  اثبات صحتها بعدة طرق منها الرسم البياني و حساب القيم




يمكنك الان اثبات صحتها من خلال هذا النشاط المعد بتقنية
 TI-nspire
لاحظ احد صفحات هذا التطبيق حيث تغير المؤشر حتى ينطبق المنحنيان على بعضهما
عند تطابق المنحنيان يشكل معادلاتهما متطابقة صحيحة دائما

هذه الصفحة لاثبات صحة المتطابقة ( sin(-x)= - sin (x







هذه الصفحة لاثبات صحة المتطابقة ( cos(-x)= - cos (x

هذه الصفحة لاثبات صحة المتطابقة ( tan(-x)= - tan (x











 في هذه الصفحة تغير المؤشر و ترى الزاوية θ   و معكوها
θ-  ,  و في الجزء الايمن من الصفحة حساب جميع النسب المثلثية الاساية للزاويتين ليستطيع الطلاب اكتشاف العلاقة بينهما و تحديد المتطابقة











 الصفحة التالية لاثبات صحة tan(x)^2= sec^2(x)-1

الصفحة التالية لاثبات صحة المتطابقة
  (sin(x) = cos(((π)/(a))-x

لتحميل الدرس المعرب انضم الى مركز تبادل أنشطةTI-nspire بالعربي على facebook

اقرأ المزيد;

قانون الجيب

حمل هذا التطبيق و اعط لطلابك فرصة لكي يكتشفوا قانون الجيب و جيب التمام و العلاقات بينهما للمزيد عن هذا التطبيق ، انقر الرابط التالي : http://goo.gl/Cy8fn

اقرأ المزيد;

النسب المثلثية

كيف تقنع طلابك ان هناك نسبة ثابتة  لا تتغير أو أن هناك عدد ثابت لا يتغير ؟؟!!

أحد هذه الامثلة هو النسب المثلثية فالمثلث القائم الزاوية الذي يحوي أحد زواياه 50 درجة مثلا لا تتغير حاصل قسمة مقابله على وتره و هو ما يعرف بالجيب للزاوية 50 مهما تغيرت أطوال المثلث القاسم و لكن كيف نقنع طلابنا بذلك ؟؟

الان بتقنية TI-Nspire  يمكنك انشاء أوراق عمل تفاعلية تسمح لطلابك بتغيير ماتريد و بقاء ماتريد ثابتا ، مثل هذا التطبيق المعد عن المثلث القائم الزاوية الذي يحوي زاوية 50 و يسمح للطلاب بتغيير الاطوال دون تغيير الزوايا و يحسب النسبة المطلوبة

يمكنك تحميل النشاط و ملاحظات عنه و أوراق العمل الخاصة به من الرابط التالي :

انقر هنا لتحميل الرابط 

شاهد الفيديو التالي و المصور عن التطبيق المعد بتقنية  TI-Nspire 

اقرأ المزيد;

وسائل ايضاح تفاعلية باستخدام تقنيىة TI-NSPIRE

في تقنية TI-NSPIRE يمكنك انشاء وسائل ايضاح تفاعلية تمكن الطالب من استنتاج العلاقات لوحده تعزز مفهوم التعلم الذاتي و تراعي الفروق الفردية بين الطلبة بحيث يتعلم كل طالب حسب سرعته الخاصة
في هذا المثال ربط المعلم بين ايجاد قيمة جيب الزاوية و جيب تمام الزاوية و التمثيل البياني لها

يمكنك تحميل الدرس كاملا بتقنية TI-NSPIRE  من الرابط التالي

اقرأ المزيد;